Year: Fifth | Course Code: Chem.-5101 | Type: Theory | Marks: (75+25) = 100 | Credit: 4 | ||||
Course Title: Quantum Mechanics and Statistical Mechanics | Exam-2022, 2023 | |||||||
Objective of the Course: To understand, determine and solve the mechanism and functions of quantum mechanical operators. | ||||||||
Course Teacher: | ||||||||
Course Content/Description: | ILO: Upon completion of this course students will be able to- | |||||||
1. Quantum Mechanical Operators: | Concept of operators, Quantum mechanical operators and classical mechanical variables. Linear, Laplacian, Hamiltonian, Momentum, Position operators. Orthogonality, orthogonality and normalization of wave functions, Kronecker’s delta. Commuting operators, Hermitian operators and their significances. Postulates of quantum mechanics, Eigen functions and Eigen values. Dirac bracket notations. Approximate solution of Schrodinger equation: Perturbation method; Variation method and their applications. [20 lectures] | determine & compare operators & theories of quantum mechanical system. | ||||||
2. Statistical Mechanics: | a) Probability and frequency; Macrostates & Microstates; Cell, position space; Momentum space, Phase space & Phase cells; Fundamental postulates of statistical mechanics; Ensembles: Microcanonical, Canonical & Grand Canonical. b) Statistical mechanics: Systems of independent particles, Fermi-Dirac, Bose-Einstein and Boltzmann distribution laws and their comparison. [18 lectures] | determine & compare theories of statistical mechanics. | ||||||
3. Partition Functions: | Partition functions: relation to thermodynamic functions. Evaluation of partition functions: translational, rotational, vibrational, electronic and nuclear partition functions. [12lectures] | evaluate & compare different partition functions. | ||||||
4. Characteristicsof Crystalline Solids: | Thermal characteristics of crystalline solids: Einstein and Debye theories and their comparison. [10 lectures] | characterize & compare theories of crystalline solids. | ||||||
Required texts/Resources: | ||||||||
| ||||||||
Information about assignments and marks: Continuous assessment: Total marks: 25 (class attendance = 10 + class tests & assignments = 15); Final exam marks: 75; Total 60 lectures. | ||||||||
As the first example, while a mathematically precise value of the position 
 -
-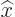 .
.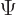
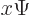 :
:
| (3.3) |
Instead of a linear momentum ![]()
![]()
![]() ,
,![]() -
-
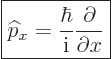 | (3.4) |
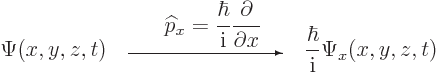 | (3.5) |
The factor ![]()
![]()
The operators ![]()
![]()
![]() :
:
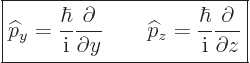 | (3.6) |
The kinetic energy operator ![]()
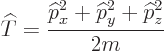 | (3.7) |
This is an example of the “Newtonian analogy”: the relationships between the different operators in quantum mechanics are in general the same as those between the corresponding numerical values in Newtonian physics. But since the momentum operators are gradients, the actual kinetic energy operator is, from the momentum operators above:
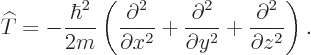 | (3.8) |
Mathematicians call the set of second order derivative operators in the kinetic energy operator the Laplacian
, and indicate it by ![]() :
:
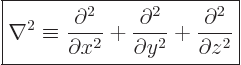 | (3.9) |
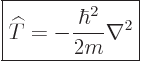 | (3.10) |
Following the Newtonian analogy once more, the total energy operator, indicated by ![]() ,
,![]() :
:
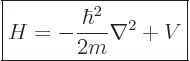 | (3.11) |
This total energy operator ![]()
![]()
![]() ,
,![]() ,
,![]() ,
,
| (3.12) |
It is seen later that in many cases a more elaborate numbering of the eigenvalues and eigenvectors of the Hamiltonian is desirable instead of using a single counter ![]() .
.![]() ,
,![]()
![]()
(It is also important to remember that in the literature, the Hamiltonian eigenvalue problem is commonly referred to as the time-independent Schrödinger equation.
However, this book prefers to reserve the term Schrödinger equation for the unsteady evolution of the wave function.)
Hamiltonian operator:
- It is the summation of the kinetic and potential energy operator.
- The operator of kinetic energy should be the same for all the models but potential energy changes as per the parameters.
- It is denoted the
The description of the Hamiltonian operator is shown below:
- It is used to calculate the system energy in terms of the wave function of quantum mechanics.
- The input of this operator is wavefunction and the output is energy in the form of eigenvalues.
- The wavefunction is the smallest amount of energy in the form of vibrational energy, also known as zero-point energy.
- It is expressed in terms of momenta and position coordinates.
- The formula for the Hamiltonian operator is:
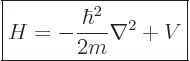
- where the first term denotes the kinetic energy and the second term denotes the potential energy. In this equation, p is momentum, m is mass, and V is potential.
- The operator is calculated in a particular direction of time.
CONSTRUCTION of OPERATOR (Click here)Hamiltonian operator:
- It is the summation of the kinetic and potential energy operator.
- The operator of kinetic energy should be the same for all the models but potential energy changes as per the parameters.
- It is denoted the
as an operator.
The description of the Hamiltonian operator is shown below:
- It is used to calculate the system energy in terms of the wave function of quantum mechanics.
- The input of this operator is wavefunction and the output is energy in the form of eigenvalues.
- The wavefunction is the smallest amount of energy in the form of vibrational energy, also known as zero-point energy.
- It is expressed in terms of momenta and position coordinates.
- The formula for the Hamiltonian operator is:
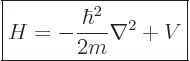
- where the first term denotes the kinetic energy and the second term denotes the potential energy. In this equation, p is momentum, m is mass, and V is potential.
- The operator is calculated in a particular direction of time.
No comments:
Post a Comment